When you’re given the graph of a function and your pre-calculus teacher asks you to find the limit, you read values from the graph — something you’ve been doing ever since you learned what a graph was! If you’re looking for a limit from the left, you follow that function from the left-hand side toward the x value in question. Repeat this process from the right to find the right-hand limit. If the y value being approached from the left is the same as the y-value being approached from the right (did the pencils meet?), that y value is the limit. Because the process of graphing a function can be long and complicated, you shouldn’t use the graphing approach unless you’ve been given the graph.
For example, find
1.1 Limits Graphicallyap Calculus 2nd Edition

What happens as we approach from the left from values less than seven 6.9, 6.99, 6.999 well it looks like the value of our function is approaching two, it doesn't matter that the actual function is defined g of seven is five but as we approach from the left, as x goes 6.9, 6.99 and so on, it looks like our value of our function is approaching. Home Calendar Zoom. 1.1 Limits Numerically & Graphically. Complete Hw Notes 1.1 Key. HW 1.1 Key mistake #3b should be -7/3. Triangles, and trapezoids—all of which can be found without calculus. If, however, we want to find areas of planar regions with curved boundaries, such as the region D in Figure 4.1.1, then we need to use calculus. Areas of Basic Regions You probably “know”that the area of a rectangle is the product of its base times its height A = bh. Proper understanding of limits is key to understanding calculus. With limits, we can accomplish seemingly impossible mathematical things, like adding up an infinite number of numbers (and not get infinity) and finding the slope of a line between two points, where the 'two points' are actually the same point.
Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more.
in the preceding figure.
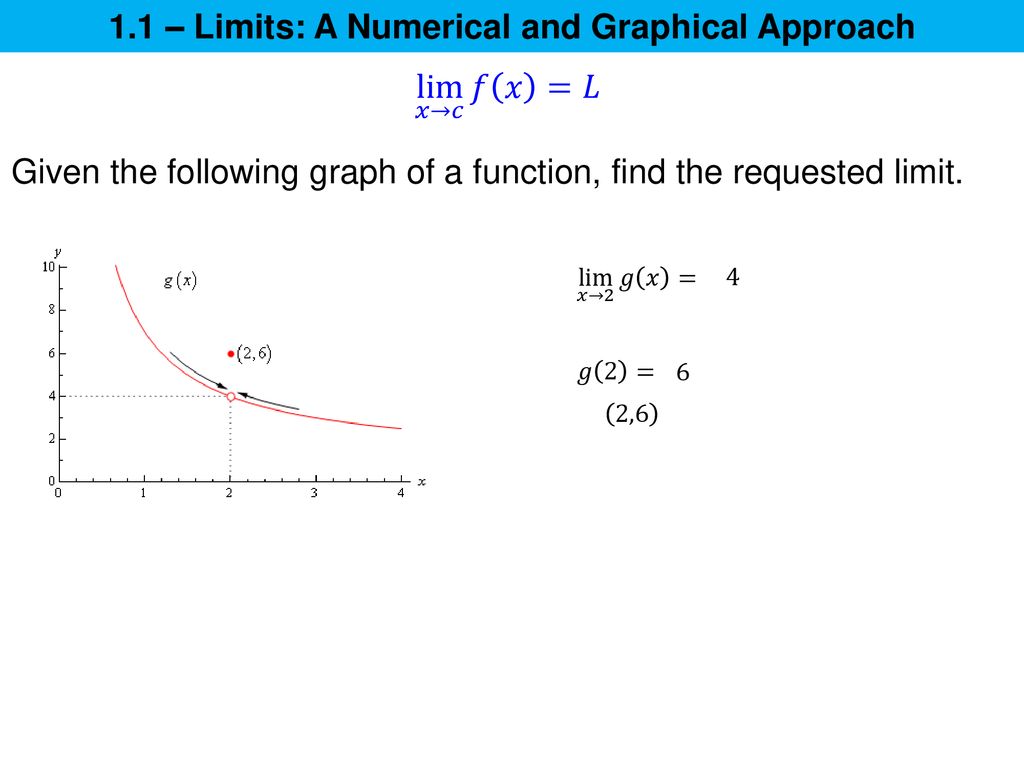
You can see that as the x-value gets closer and closer to –1, the value of the function f(x) approaches 6. And in fact, when x gets to –1, the function’s value actually is 6! Technically, though, having f(–1) = 6 isn’t required in order to say that the limit is 6; the function could have a hole in it at that point, and the limit would still be 6! See the next example:
In the graph, you can see a hole in the function at x = 3, which means that the function is undefined — but that doesn’t mean you can’t state a limit. If you look at the function’s values from the left,
and from the right,
you see that the y value approaches 3. So you say that the limit of the function as x approaches 3 is 3.
1.1 Limits Graphicallyap Calculus Calculator
You can see that the function has a vertical asymptote at x = –5. From the left, the function approaches negative infinity as it nears x = –5. You can express this mathematically as

From the right, the function approaches infinity as it nears x = –5. You write this situation as


Therefore, the limit doesn’t exist at this value, because the left-hand limit is negative infinity but the right-hand limit is infinity.
For a function to have a limit, the left and right limits must be the same. A function can have a hole in the graph at a particular x value but the limit as x approaches this value can still exist, like
2011-2012
Describe or draw a function, f(x), with the following characteristics:
- f(x) has domain (–∞,8)
- f(x) has range (–∞,9)
- f(4) = 0; f(5) = 0; f(7) = 0
- The limit, as x approaches –∞, of f(x) equals 9
- The limit, as x approaches 8 from the left, of f(x) equals –∞
- f(–1) = f(–3); f(–1) > f(–2)
- f(1) = 1
- The limit, as x approaches 1, of f(x) is 4
One Solution (others possible but similar):
The video may take a few seconds to load.Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.